December 27, 2020. Another bathroom-themed post, this time on the mysterious billowing of shower curtains. This is related to the fact that planes can fly upside down!

The case of the contrary curtain

A few days ago, I was taking a shower when I noticed the bottom of the shower curtain nipping at my heels. The bathroom window was closed, and the house was not particularly drafty, so I began to wonder if there was another explanation. Before I left the shower, I had arrived at a hypothesis: the hot water of the shower is lighter than the cold air outside, so it rises over the top of the shower curtain, cools, and pushes the column of cold air down. The cold bottom of this column slips in under the curtain.

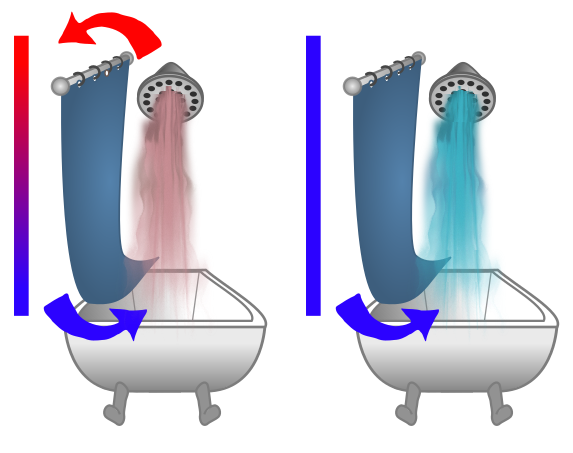
I mentioned the phenomena and proposed buoyancy mechanism to my partner. She told me she had noticed the same effect in a cold shower! In this case, there is no obvious reason for air to rise over the top of the curtain, since it’s all at the same temperature. Something else is at play!

Einstein’s wonky wing

If temperature isn’t relevant, the stream of water coming down is. Presumably, this generates a steam of air moving in the same direction, and the question becomes: why does this result in air being pushed in under the curtain? Since the air is moving, it is tempting to invoke Bernoulli’s principle, which states that in a stream of moving fluid, the sum of gravitational potential energy, pressure, and speed, is constant:

\[\frac{1}{2}\rho v^2 + \rho g + P = \text{const}.\]

Since the air is moving inside of the shower curtain, and the density should be the same, the pressure should drop inside the shower. This will result in air rushing in under the curtain. We draw a cross-section of this explanation below. On the left is the stationary air. On the right is the moving air at lower pressure, with the low-pressure region in grey. The blue arrow is the resulting force.

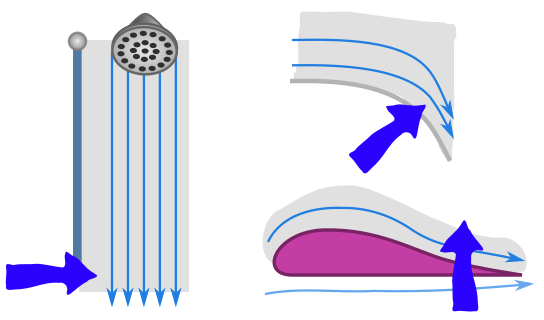
This same reasoning is used to explain why holding a piece of paper in your hand and blowing over the top of it causes the paper to rise. It’s also the conventional explanation for why planes fly. The idea is that the top surface of a wing or aerofoil is longer than the bottom, so assuming that air takes the same time to travel over the top and bottom surface, it must travel faster over the top, and once again Bernoulli’s principle seems to predict a lower pressure above and hence an upwards lift.

All of these explanations are wrong. As this xkcd succinctly points out, planes can fly upside down, while the Bernoulli explanation predicts that lift now points in the wrong direction. This is a subtle problem, and deceived no lesser a scientist than Albert Einstein, who was hired by a German aircraft manufacturer during WWI to design a better aerofoil. He added a hump in the middle of the wing to increase the surface area, assuming this would increase lift due to the conventional Bernoulli model, but it flopped in wind tunnel experiments.

Similarly, if you blow too closely to the piece of paper, it doesn’t rise. I couldn’t repeat this experiment with the showerhead, but Australian physics teacher Peter Eastwell did, finding that if the stream of water is too close to the curtain, it does not billow. This is inexplicable if we believe the Bernoulli model, since the pressure should be even lower (since the stream is closer to the surface) and the force therefore stronger. Once again, it’s back to the drawing board!

Entrainment and the Coandă effect

Bernoulli’s equation only applies when viscosity—“stickiness” between layers of fluid—is negligible. But in all the situations above, viscosity plays a key role. The basic idea is very simple. A narrow stream of air will tend to pull nearby air along with it due to stickiness. Carrying off air particles will create a partial vacuum, i.e. a region of reduced pressure. If you want to be precise, you can note that the ideal gas law

\[PV \propto NT\]

tells us that, if volume $V$ and temperature $T$ are kept fixed, then reduced particle number $N$ reduces pressure $P$. The process of glomming nearby air onto the stream is called entrainment.

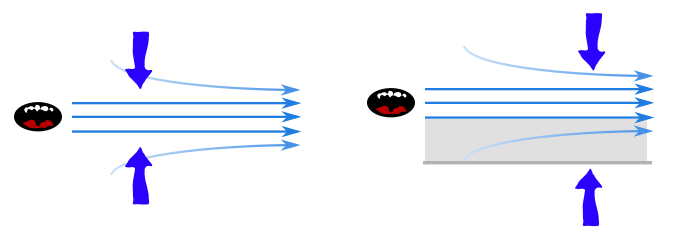
Nature will try to fill up these low-pressure regions with air at atmospheric pressure. But if there is an obstruction on one side, this side cannot equalise to atmospheric pressure, since the air can’t pass through the obstruction. So the region between the obstruction and the air stream remains at low pressure. There are two things that can happen, and they are not mutually exclusive. If the surface is flexible, the air on the other side can push it towards the low pressure region. This is what we see with the shower curtain and the piece of paper.

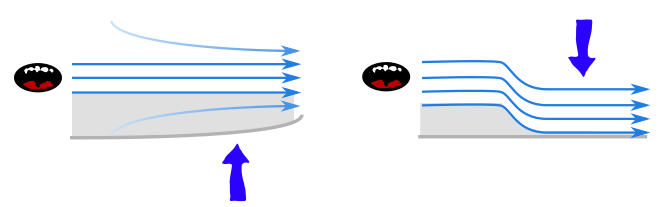
But if the surface cannot come to the air stream, the air stream will go to the surface, with atmospheric pressure simply pressing it through the low pressure and onto the surface. This phenomenon is called the Coandă effect after Romanian inventor Henri Coandă, though it was described eloquently a century earlier by polymath Thomas Young:

The lateral pressure which urges the flame of a candle towards the stream of air from a blowpipe is probably exactly similar to that pressure which eases the inflection of a current of air near an obstacle. Mark the dimple which a slender stream of air makes on the surface of water. Bring a convex body into contact with the side of the stream and the place of the dimple will immediately show the current is deflected towards the body; and if the body be at liberty to move in every direction it will be urged towards the current…

Flying upside down

The Coandă effect helps explain why planes fly upside down. The air passing by the aerofoil or wing is entrained and redirected along the curves. If this air is directed downwards, then Newton’s third law ensures that lift is generated. If the plane is upside down, lift is generated in exactly the same way. In the images below, the plane is flying to the left, and the blue arrow represents the reaction force on the plane. The vertical component is lift.

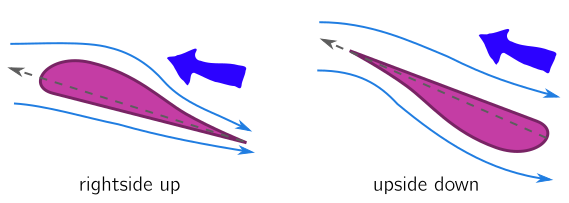
Clearly, the plane needs to be angle so that the redirected air is pointing down. The angle made between the line of the wing (grey line above) and the horizontal is called the angle of attack. A good angle of attack is crucial for flight. If the angle is too small, the plane stalls, meaning that the lift generated is not sufficient to keep the plane in the air. If the angle is too large, it splits the air off into two streams, and creates a partial vacuum which fills in with turbulent eddies, a process called cavitation.

You might think that cavitation could provide more lift, but the turbulence wobbles the wings, and redirects energy from lift into vibrating the aerofoil. Turbulence on an airliner worries passengers because it’s uncomfortable, but the pilot because it might stop the plane from flying! On the other hand, cavitation can provide short-term lift. In fact, as Peter Eastwell points out, strong winds rushing over the top of a gabled roof cavitate, and the resulting pressure difference can rip the roof off! As Einstein’s bungle suggests, to optimize the performance of an airplane wing, we need the right model for how it works. The aerodynamics of entrainment and cavitation are complicated topics, but the humble shower curtain a surprisingly good place to start!