December 13, 2020. A short, equation-free post on the fun physics of hairy shadows.

Place a human hair on a body of water in a well-lit bathroom. Any part of the hair which pierces the water will cast an ordinary geometric shadow. But the parts that rest on the surface cast a blotchy, large shadow, surrounded by bright fringes. I decided to investigate after my brother asked me why it happens!

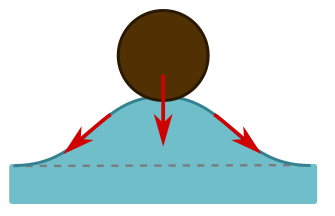
The short answer is surface tension. The molecules at the surface of the water are more strongly attracted to each other than the molecules in the middle, since they have nothing to attach to above. So they form a sort of elastic membrane on which the hair can sit. Often, the explanations of how surface tension works are confusing and wrong. If the membrane is unbroken, how can it pull on an object? Basically, it’s a spring, and stretching it will produce a restoring force along the spring. This can generate an upwards force on the object if it sits in a dip, as the angled arrows indicate below left.

But when we displace water, as in this dip, buoyancy forces due to the weight of displaced water trying to push its way back also play a role. They provide an upward force, also shown above left. The force due to buoyancy is the volume of the hair beneath the water level (the dotted line above right). But we have displaced some extra water, shown in purple, and this turns out to precisely equal the effects of surface tension. It is the total weight of displaced water that pushes on the membrane formed by surface tension, so that we have a nice generalisation of Archimedes’ principle:

The force on an object supported by surface tension is the weight of displaced water.

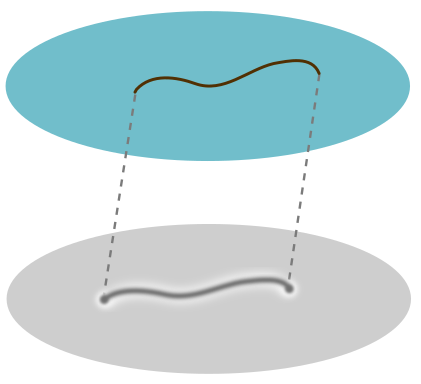
Now we can explain the odd shadow. The dip creates a concave lens which makes the light diverge, leading to a larger shadow. To return to a flat, level surface, it must undo some of the concave curvature with some convex curvature at the edges. This is what causes the bright fringe for the larger shadow. We draw a cartoon below, with edges of the concave and convex sections represented by dots:

The blotchiness is to do with the fact that hair has “torsion”, i.e. it likes to curl and kink and do other things. This means some parts will push harder on the surface than others, creating larger and smaller dips and hence blotchy shadows.

But this isn’t the end of the story. I noticed that if I grabbed the hair at either end, and dipped one end in the water and held another in the air, the point it pierces the water casts a peculiar shadow I call a “jellyfish”:

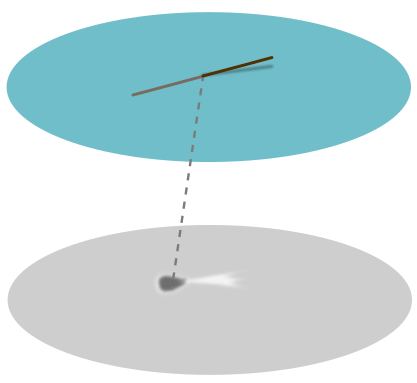
The dark part we can explain using the concave dip as above, but what about the white tail of the jellyfish? This suggests that the hair is pulling the water up with it. This doesn’t make sense if we interpret the surface as an unbroken membrane. A more reasonable picture is the following largely convex lump:

Once again, the hair in this position will be subject to a force equal to the weight of the water pulled up. I counteract that force with my own, by suspending one end in the air. So have been missing a piece of physics: the attraction between the water and the substance (keratin) making the hair. This leads to an angle of contact between the hair and the water, most convenient to visualise by placing a drop of water on a surface of hair (rather than the other way round):

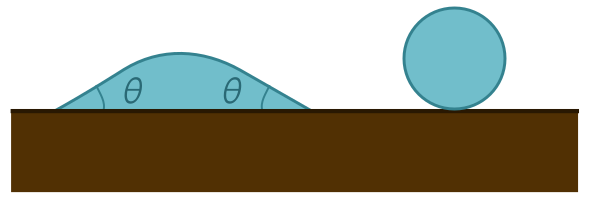
Our earlier pictures with the unbroken membrane assume the contact angle is $\theta = 180^\circ$, corresponding to a droplet with an unbroken surface, as above. In general, a surface with $90^\circ < \theta < 180^\circ$ is said to be hydrophobic, or “water-fearing”. A material with $\theta < 90^\circ$ is hydrophilic, or “water-loving”. In the extreme limit of $\theta = 0^\circ$, the drop completely spreads out over the surface, as we would expect for a maximally hydrophilic material.

Let’s return to our follicular folly. The jellyfish tells us that the contact angle for hair is smaller than $180^\circ$. To tell whether it’s hydrophilic or hydrophic, we can conduct a simple experiment. If we place the hair vertically into the water, we are doing some similar to our contact angle picture. The water will form a sort of reverse meniscus around the hair:

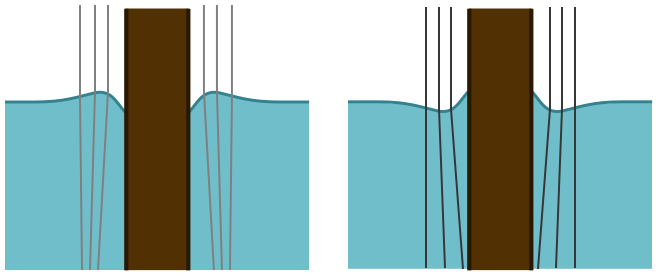
Since there is no up or down force, the volume of water above the water line should balance the water below the hair. If the contact angle is greater than $90^\circ$, and the hair is hydrophobic, then it will form a convex lens and create a small bright spot. If the contact angle is less than $90^\circ$, and the hair is hydrophilic, it will form a concave lens and make a larger dark spot.

The experiment reveals a bright spot, suggesting that hair is hydrophobic. This makes sense: hair is much less useful for keeping you warm if it absorbs water! For confirmation, I looked online for the contact angle and found that, according to the industrial scientists who design shampoo, $\theta \approx 100^\circ$. The meniscus formed around the hair, or any vertical sample, can indeed be used to measure contact angles, though the lensing of light is not the most practical means. But it is neat that by simply looking for a light or dark spot, we can learn something about the chemical properties of hair!