Pairing random socks
December 27, 2020. If you have a jumbled pile of socks, how many do you need to draw on average before getting a pair? The answer turns out to be surprisingly tricky!
Searching for socks
After a load of washing, I sometimes get lazy and throw unpaired socks into a drawer. Later, I will simply withdraw socks at random until I get a pair. Faced with this dilemma, I wondered: for $n$ pairs, what is the average number of draws required to get a pair? This simple question turns out to be surprisingly tricky to answer!
To start with, we can calculate the probability that after $k$ draws, you have no pair. This will simply be the number of ways of drawing $k$ socks with no pairs divided by the total number of ways to draw $k$ socks from the total number, $2n$. Since we have to choose $k$ distinct pairs to draw from, and within each pair there are two options, the number of ways to draw $k$ sock without a pair is
\[2^k k! \binom{n}{k} = \frac{2^k n!}{(n-k)!}.\]Thus, the probability that no pairs are drawn is
\[p_k = \frac{2^k n!}{(n-k)!} \cdot \binom{2n}{k}^{-1} = \frac{(n!)^2}{ (2n)!} \cdot 2^k\binom{2n-k}{n-k}.\]We have tried to simplify the $k$ dependence so there is a single binomial coefficient. Note that $p_k = 0$ for $k \geq n + 1$. This reflects the fact that as you soon as you have drawn more than half the socks, you are guaranteed a pair by the pigeonhole principle. Let $D$ be the number of draws needed to get a pair. Then
\[p_k = \Pr(D > k).\]We can use this to find the probability that we get a pair after exactly $k$ draws:
\[\Pr(D = k) = \Pr(D > k - 1) - \Pr(D > k + 1) = p_{k-1} - p_{k+1}.\]We can evaluate this more explicitly, but this will end up being a distraction from our main goal: to compute the average number of draws to get a pair. Since we have an expression for the probabilities $\Pr(D = k)$, we can go ahead and compute the average:
\[\langle D\rangle = \sum_{k = 0}^n k \cdot \Pr(D = k) = \sum_{k = 0}^n k \cdot (p_{k-1} - p_{k+1}). \tag{1} \label{sum}\]A hypergeometric hack
To make progress on this sum, we can use a trick. We note that each term $p_k$ occurs twice, first with a multiplier $k+1$, then a multiplier $-(k+2)$. Combined, each term appears precisely once! Thus, we can simplify the sum to
\[\langle D\rangle = D_n = \sum_{k = 0}^n p_k = \sum_{k = 0}^n \frac{(n!)^2}{ (2n)!} \cdot 2^k\binom{2n-k}{n-k}.\]This is a difficult sum, and there is (as far as I know) no closed form expression in terms of elementary functions. Instead, we can invoke a special function called the Gauss hypergeometric function to package things nicely. As nicely described in Concrete Mathematics, the hypergeometric function captures any sum whose terms differ by a rational function of $k$. More precisely, the rule is that if we have terms $t_k$ for $k \geq 0$, with a ratio
\[\frac{t_{k+1}}{t_k} = \frac{z (k+a)(k+b)}{(k+c)} \cdot \frac{1}{k+1},\]then we can package the sum of the terms into a hypergeometric function:
\[\sum_{k\geq 0} t_k = t_0 \cdot {}_2 F_1(a, b; c; z).\]There is a more general version of this relation which lets us package things into the generalized hypergeometric function but we won’t need that here. Let’s apply the relation above to the randomly drawn socks $(\ref{sum})$. The ratio of the terms $p_k$ is (after a little algebra) seen to be
\[\frac{p_{k+1}}{p_k} = \frac{2 (k-n)(k+1)}{(k-2n)} \cdot \frac{1}{k+1}.\]Note that $p_0 = 1$, since it is certain you cannot draw a pair after drawing a single sock. Thus, the average number of socks you need to randomly draw from a pair from $n$ jumbled pairs is exactly
\[\langle D\rangle = {}_2 F_1 (-n, 1; -2n; 2). \label{hyper} \tag{2}\]Simulating socks
As a sanity check, we can simulate the random drawing of socks and see that the answers agree with our formula. Here is a scatterplot of the data for $n = 1$ to $n = 20$ pairs of jumbled socks, with red datapoints obtained from simulations, and blue from the analytic expression $(\ref{hyper})$. It’s a pretty good match, and gets better as you increase the number of simulations:
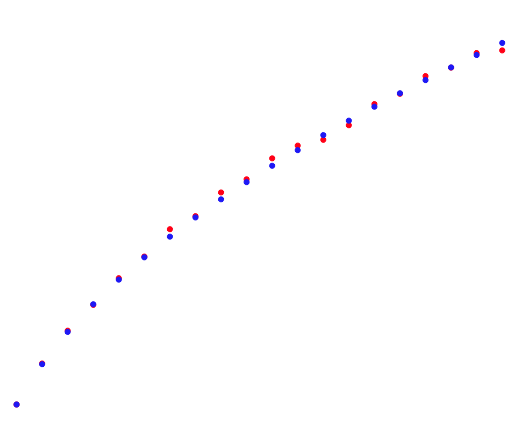
If you’re interested, here is the Python code that generates this plot:
import numpy as np
import scipy.special as sc
import matplotlib.pyplot as plt
def randsocks(n):
socks0 = [[i, 0] for i in range(n)]
socks1 = [[i, 1] for i in range(n)]
rand = np.random.permutation(socks0+socks1)
firstrand = [i for [i, j] in rand]
k = 0
while len(firstrand[:k]) == len(list(set(firstrand[:k]))):
k = k + 1
return k
averages = []
repeats = 1000
for n in range(1,21):
results = []
for rep in range(repeats):
results.append(randsocks(n))
av = sum(results)/float(len(results))
averages.append(av)
hyper = []
for n in range(1, 21):
hyper.append(sc.hyp2f1(1, -n, -2*n, 2))
fig=plt.figure()
ax=fig.add_axes([0,0,1,1])
ax.scatter(range(1,21), averages,color='r')
ax.scatter(range(1,21), hyper,color='b')
plt.show()
Alien feet
Lazy aliens might encounter the same problem I did, but with a difference: they have more than two feet! In this case, our answer above generalizes in a nice way. If the alien has $f$ feet, and draws with replacement from $n$ sets of $f$ socks, then the probability that it has no sets after $k$ draws is
\[p_k = \frac{(n!)^2}{(fn)!} \cdot f^k\binom{fn-k}{n-k}.\]The same trick can be used to evaluate the expected number of draws, $\langle D\rangle$, and we end up simply replacing $2$ with $f$ in our expression $(\ref{hyper})$:
\[\langle D \rangle = \sum_{k=0}^n p_k = {}_2 F_1 (-n, 1; -fn; f).\]We can check numerically that this increases as $f$ gets bigger, just as you might expect. Pluripedality may have its advantages, but when it comes to drawing socks from a giant disorganized pile, monopods have a leg up.
Biographical postscript
When I was 10 or so, my older sisters gave me a copy of Math Curse, a picture book about someone who sees math problems everywhere. Clearly, I have fulfilled their prediction and become a math zombie!