January 10, 2021. I discuss the mathematics of Spot It! (aka Dobble in the UK) and its various generalisations, including projective planes, combinatorial designs, and an entertaining polytopal turducken.

Introduction

Spot It! (called Dobble in the UK) is a simple card game based on some relatively deep mathematics. There is a deck of $55$ cards, each of which has eight symbols printed on it, from a total symbol vocabulary of $57$. For each two cards in the deck, there is precisely one symbol in common, and on each round, the first person to find the shared symbol between the last card and a newly drawn card wins a point. Eight is a good number since, according to Miller’s “law”, the number of objects the average human can hold in short-term memory is seven.

You can play an online version by Ken Wessen. I enjoy the game, but like many mathematically-minded folk who encounter it, became increasingly distracted by the question: how does it work?

Finite projective planes

The game requires that every two cards share precisely one symbol in common. If we add the further constraint that each pair of symbols occurs on one card only, then we have a nice equivalence to the finite projective plane, provided we interpret a card as a line and a symbol as a point at which lines intersect, since our constraints become the “axioms”:

1. Any two lines (cards) intersect at exactly one point (symbol).
2. Any two points (symbols) are joined by exactly one line (card).

Our question becomes about the existence of finite projective planes. There is a constructive approach, nicely outlined by Yuval Filmus, which yields the game as a special case. Let $p$ be a prime number, and consider the finite field $\mathbb{Z}_p = \{0, 1, 2, \ldots, p - 1\}$, viewed as $p$ nodes on a circle. (You can generalise to prime power fields, but we’ll stick with primes for simplicity.) We picture $p = 3, 5, 7$ below:

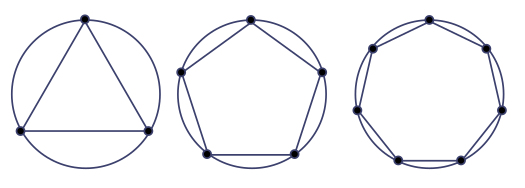
To make a projective plane out of $\mathbb{Z}_p$, you do two things: make it projective and make it a plane. “Projective” means we add a point at infinity $\infty$, giving $\mathbb{Z}_p^* := \mathbb{Z}_p \cup \{\infty\}$. “Plane” means we consider all pairs made from $\mathbb{Z}_p^*$, subject to the proviso that $(m, \infty) \overset{S}{\sim} (\infty, m)$, where $S$ is the relation. Modding out by $S$ leads to the projective plane

\[\mathcal{P}_p = (\mathbb{Z}_p^* \times \mathbb{Z}_p^*)/S,\]

with

\[|\mathcal{P}_p| = n = (p+ 1)^2 - p = p^2 + p + 1.\]

Here are the steps for $p = 3$:

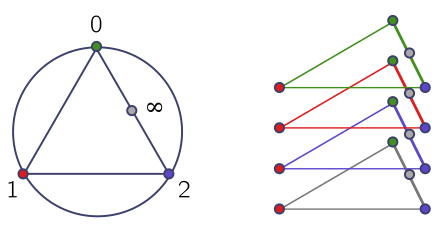
In the first figure, we add the grey point “at infinity” (which occurs after $2$). In the second figure, the $x$ coordinate is given by the colour of the node and the $y$ coordinate by the colour of the triangle it lies on. Note that the coloured points on the grey triangle are equivalent to the corresponding grey points on the coloured triangle. A line in this geometry is very similar to a line in the Cartesian plane, and defined as something with a finite slope and finite $y$-intercept, or a vertical line with a (possibly infinite) $x$-intercept:

\[y = mx + c \text{ or } x = a.\]

We illustrate for $p = 3$ once more. Note that for the lines with finite slope and intercept, it’s convenient to use points on the grey triangle, while for the vertical lines, it’s more convenient to use grey points:

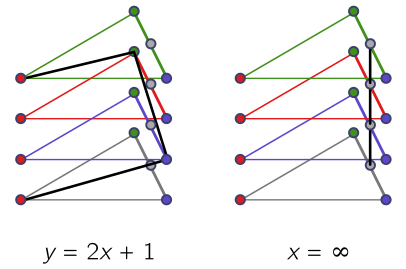
For finite slope and intercept, $m, c \in \mathbb{Z}_p$, while $a \in \mathbb{Z}_p^*$, so the total number of lines is

\[d = p^2 + p + 1,\]

precisely the number of points. We might have expected this from the fact that in the axioms, the role of lines and points are interchangeable! Spot It! realises this construction for $p = 7$, with $n = 7^2 + 7 + 1 = 57$ symbols. We can now easily draw a picture of the corresponding projective plane:

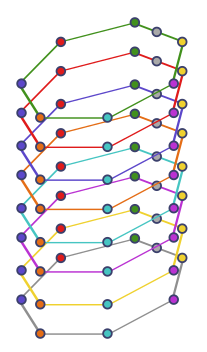
Each card is a line with $p + 1 = 8$ symbols. For some mysterious reason, the designers removed two cards, so $d = 55$ rather than $57$. Speculation on the internet is rife, and I remain agnostic. But ignoring this mutilation, Spot It! is really just a projective plane built out of the finite field $\mathbb{Z}_7$. I also can’t resist sharing the smallest example, $p = 2$, which leads to a beautiful object called the Fano plane. The conventional representation is connected to our picture by the following sequence of transformations:

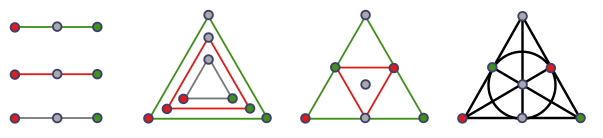
Draw each row as a triangle, and nest them rather than stacking them. Get rid of the copied points on the grey triangle, then rotate the red triangle so it hits the outer green triangle with three colours along each edge. Now draw all the lines, and you have the Fano plane! (This construction also works if you have the grey triangle on the outside and get rid of the grey points.) Technically, this is a graph of the points, with an edge just in case they lie on some line together, called the incidence geometry.

We’ll show below that, for any projective plane, it must be the case that $n = q^2 + q + 1$ for some number $q$ which is one less than the number of symbols per card. It is conjectured that $q$ must be a prime power, which completely solves the projective plane generalisation of Spot It!. But this construction fixes certain features that strike me as unnatural. First, we added the constraint that any pair of symbols appears on precisely one card. Why not two, or three, or no constraint at all? Or dually, why not allow for an overlap of more than one symbol? The answers won’t be projective geometries. But they may still be interesting!

Combinatorial designs

We’ll start with constraints on co-occurence. Consider a deck of $d$ cards, with an alphabet of $n$ symbols, and $k$ symbols per card. Further, suppose each symbol appears on $r$ cards, and each given pair of symbols appears in $\lambda$ distinct cards. The resulting arrangement is called a $2$-$(n, k, \lambda)$ combinatorial design, or $2$-design for short. We don’t bother to list $r$ or $b$ since they are determined by the other parameters according to

\[dk = nr.\]

The proof is simply that the LHS counts the total number of symbols (with multiplicity) by card, and the RHS by symbol. In general, Fisher’s inequality states that $d \geq n$, a result we will prove somewhat unconventionally at the end of the post. The restriction to $d = n$ but arbitrary $\lambda$ is called a symmetric 2-design, and the projective plane is the special case $\lambda = 1$. We can say a little more about these symmetric designs. A basic contraint is that

\[\lambda (n - 1) = k(k - 1),\]

since both sides count the total number of pairs (with multiplicity), divided by $n$, with the LHS counting by co-occurrence of symbols, and the RHS from cards (using $k = r$ for a symmetric 2-design). Setting $\lambda = 1$ for the projective plane, and writing $q = k - 1$,

\[n = k(k - 1) + 1 = q(q+1) + 1 = q^2 + q + 1,\]

so that the form of $n$ is necessary, and $q + 1$ is one more than the number of symbols per card. Finally, you might ask about the $2$ in $2$-design. It turns out there is a generalisation called a $t$-design, where instead of having every pair appear $\lambda$ times, you have every $t$-element subset of the alphabet appear on $\lambda$ cards. I won’t say more about them, but just wanted to point out they exist and constitute an even broader generalisation.

Sets and polytopes

I’ll end with yet another generalisation which occurred to me before reading about projective planes or designs. The basic observation is that we can view a card as a feature vector $\mathbf{v} = (v_i) \in \mathbb{R}^n$, where $i = 1, 2, \ldots, n$ label symbols in the alphabet. We choose a convention where $v_i = 1$ if $i$ is on the card and $0$ otherwise. As an example, if $n = 4$ and the card contains symbols $1$ and $2$ but not $3$ and $4$, it is represented by a vector $\mathbf{v} = (1, 1, 0, 0)$. In this representation, the size $k$ of a card is related to the length of the vector: if there are $k$ symbols on a card, then $k$ entries $v_i$ equal $1$, and hence

\[|\mathbf{v}|^2 = \sum_i v_i^2 = k \quad \Longrightarrow \quad |\mathbf{v}| = \sqrt{k}.\]

In this setup, it’s natural to consider an overlap of $c$ symbols per card. This can be easily expressed in terms of the dot product, and hence angle between vectors:

\[\mathbf{u} \cdot \mathbf{v} = \sum_i u_i v_i = c \quad \Longrightarrow \quad \cos\theta = \frac{\mathbf{u} \cdot \mathbf{v}}{|\mathbf{u}| |\mathbf{v}|} = \frac{c}{k}.\]

A deck of $d$ cards satisfying this condition has a pleasingly convoluted geometric interpretation. First, since the entries are binary, each card is a vertex of the unit hypercube in $n$ dimensions:

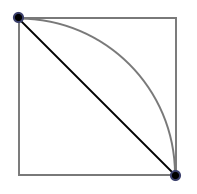
\[\mathbf{v} \in H_n = \{0, 1\}^n.\]

Second, since they all have length $\sqrt{k}$, they lie on the intersection of $H_n$ with the hypersphere of radius $\sqrt{k}$. Finally, since they all are separated by an angle $\theta = \cos^{-1}(c/k)$, they are separated by constant distance. It’s easiest to see this by simply measuring the arclength along the hypersphere, which is $s = \sqrt{k}\theta$. Since the $d$ points are pairwise separated by the same distance, they form a $(d-1)$-simplex. Since this simplex lies on both a hypersphere and a hypercube, it’s a sort of polytopal turducken! We give a simplexample for $n = 2$:

We can assemble the vectors in a deck into the rows of a matrix, called the incidence matrix. Here, for instance, is the Fano plane, now realised as a $6$-simplex in $\mathbb{R}^7$:

\[\left[ \begin{matrix} 1&0&1&1&0&0&0 \\ 1&0&0&0&1&0&1 \\ 1&1&0&0&0&1&1 \\ 0&1&0&1&0&0&1 \\ 0&1&1&0&1&0&0 \\ 0&0&1&0&0&1&1 \\ 0&0&0&1&1&1&0 \end{matrix} \right].\]

There is a nice scheme for generating decks as follows. Select a deck size $d$, and for the set $D = \{1, 2, \ldots, d\}$, select all subsets of size $r$, $D_r = \binom{D}{r}$. We now make an alphabet where each symbol corresponds to an element of $D_r$, so

\[n = \left|\binom{D}{r}\right| = \binom{d}{r} = \frac{d!}{(d-r)!r!}.\]

Our incidence matrix will have $d$ rows and $n$ columns. Each column corresponds to a subset $s_i$, with $1$ in row $a$ just in case element $a\in D$ is in $s_i$. Otherwise, it is $0$. Here is an example for $d = 4$ and $r = 2$:

\[\left[ \begin{matrix} 1&1&1&0&0&0\\ 1&0&0&1&1&0\\ 0&1&0&1&0&1\\ 0&0&1&0&1&1 \end{matrix} \right].\]

Converting to a deck, cards correspond to row vectors $\mathbf{v}^{(a)}$ and symbols to columns. The length squared of a vector, or the number of symbols per card, is

\[k = \binom{d - 1}{r - 1},\]

since if we fix a $1$ in some position, $k$ is the number of ways to assign the remaining $r - 1$ unit entries in each column, which is realised as $k$ unit entries per row. Similarly, it’s not hard to see that any two cards generated this way overlap at $c$ points, for

\[c = \binom{d - 2}{r - 2}.\]

If we fix that two vectors both contain some $b \in D$, for instance, then this $c$ is the precisely the number of ways we can arrange the remaining $r - 2$ unit entries to form a set, which will be realised as $c$ overlaps between rows. You can generalise to shared triples and so in the obvious way. The number of distinct decks that can be generated this way is the number of ways of permuting symbols, $n!$, divided by the number of ways of permuting rows, $d!$, since these will simply reorder cards without changing the deck:

\[N_{d, r} = \frac{n!}{d!} = \frac{\binom{d}{r}!}{d!}.\]

This approach is related to the beautiful combinatorics of set intersections. But I’ll leave that for another time, and instead finish with a simple observation about simplices. A $(d-1)$-simplex is built from $d$ points with the same pairwise separation. It’s only possible to embed points these points when you have (at least) $d - 1$ dimensions at your disposal: for each point you add, you need to treat the previous points as a lower-dimensional simplex “base” and place the new point in an orthogonal dimension where it can equidistant from each point in the base. Since the hypersphere in $\mathbb{R}^n$ has $n - 1$ dimensions, we learn that $d \leq n$. This has a nifty consequence. First, it’s easy to check that our incidence matrices actually satisfy the conditions for the transpose of an incidence matrix of a $2$-design, with the relation between columns and rows swapped. Our observation about simplices then implies that for a $2$-design, $d \geq n$, and hence gives a geometric proof of Fisher’s inequality!

Resources

• “What is the math behind the game Spot It!?” (2011), Mathematics StackExchange.
• “The mathematics of Dobble” (accessed 2021), Ken Wessen.