December 2, 2022. Humans are the measure of all things, though not in the sense Protagoras meant. I show how to estimate distance using only your hands and feet.

Introduction

---

The Greek philosopher Protagoras famously stated that “man is the measure of all things”. He was also skeptical about whether math could be applied to the real world. According to Aristotle, he arged that “perceptible lines are not the kind of things the geometer talks about”. We’ll make a bad Protagoran joke and use humans, the “measure of all things”, to measure distances by exploiting the geometry of “perceptible lines”.

Theory

---

So, consider a distant object you want to find the distance to. Hold your hand out at a fixed distance from your eyes and fixed orientation (e.g. horizontal), and estimate the size of the object in fingers $f$. (For best results, use an integer number of fingers.) Your arm and hands form a triangle which is similar to the triangle formed by the distant object:

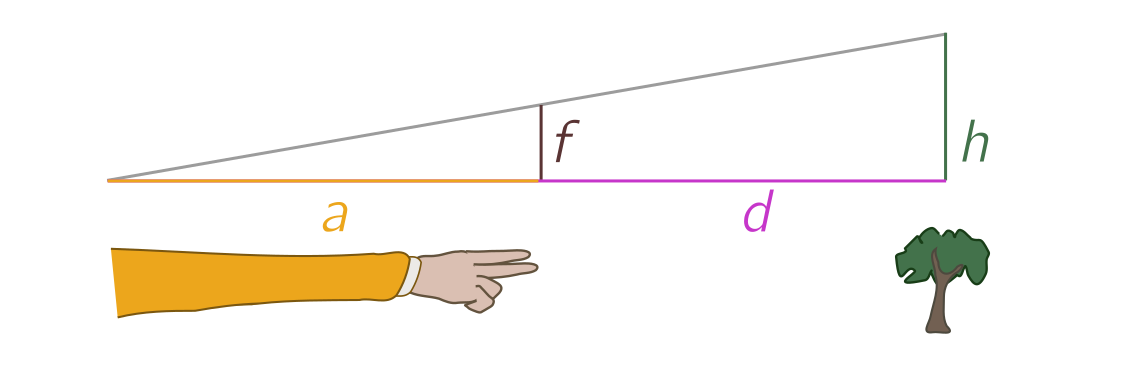
If $a$ is the length of your arm, $h$ the actual height, $d$ the distance to the object and $f$ the apparent height in fingers, then

\[\frac{f}{a} = \frac{h}{d}. \tag{1} \label{f}\]

Now walk $s$ steps towards the object, so that it has finger width $f’$. We now have a new set of similar triangles:

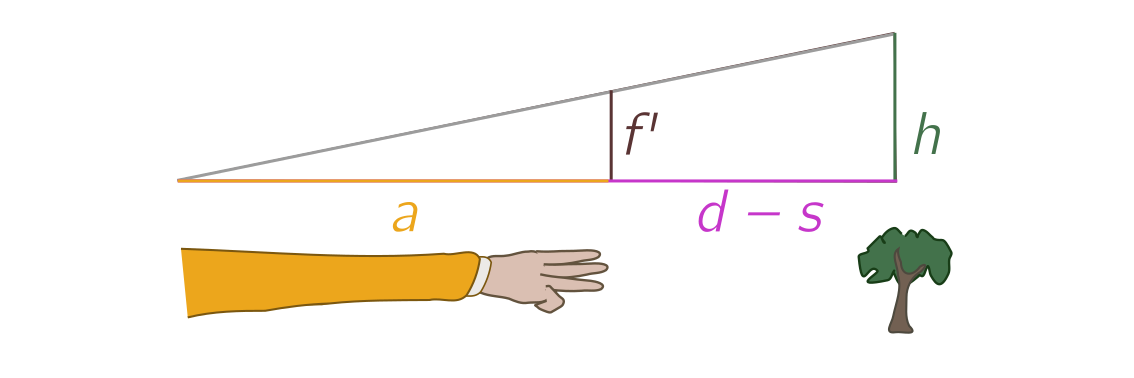
The ratio of sides now obeys

\[\frac{f'}{a} = \frac{h}{d-s}, \tag{2} \label{fdash}\]

where we measure distance in steps. We can rearrange $(\ref{f})$ and $(\ref{fdash})$ to eliminate the length of the arm, $a$, and physical height $h$, to find a method for distance measurement about which Protagoras might have mixed feelings.

Practice

---

Take the transition from $f = 3$ to $f’ = 4$. In this case, the distance estimate is

\[d = \frac{s}{1 -(f/f')} = \frac{s}{1 - 3/4} = 4s,\]

or four times the number of steps. I find this works with $90$-$95\%$ accuracy for distances on the order of $50$ steps. I suspect that varying finger width and step length are the main source of error; arm length $a$ can be fixed by maximally extending the arm, and orientation of the hands can be fixed by a reference line, e.g. the horizon.

Beyond varying width, the main disadvantage of fingers as a measurement device is their resolution. By counting the number of steps from $f = 9$ to $f’ = 10$, you estimate $d \approx 10s$, but that is the best you can do. For large ratios, you need to replace fingers with a finer measurement instrument, such as a clear plastic ruler held at arm’s length. Although you will get better results and enable yourself to measure larger distances, you may look a tad eccentric. But as Protagoras informs us, that is a tradeoff that each individual must assess themselves.

Extension

---

It’s simple to extend this method to estimate height. Once $d$ is known, we can use $(\ref{f})$ to give the physical height (or width, or whatever we’ve measured) in terms of other quantities:

\[h = \frac{df}{a}.\]

Now, if we know $a$ in finger lengths, we will get an estimate of the height in steps. That’s a bit silly, so I suggest learning your arm length, finger width, and step size in meters. But note that, for an order of magnitude guess, one step is around $1.2$ arm lengths, so the height is $1.2$ times the number of steps times the finger span.

Example: I estimated a car had size $f = 3 \text{ fingers} \approx 4 \text{ cm}$ at a distance $d = 40$ steps. This leads to a height estimate

\[h \approx 40 \times 1.2 \times 4 \text{ cm} \approx 1.9 \text{ m},\]

which is probably an overestimate but in the right ballpark. Once again, a ruler leads to more accurate results at the cost of visible dorkiness.