February 3, 2021. Bla bla bla

Introduction

Black holes are regions of spacetime where gravity is strong enough to trap light. Now, light travels pretty fast, about a hundred million times faster than a speeding pedestrian, so this is no mean feat, and it takes the death of a giant star, or disastrous collisions at the core of a galaxy, to produce them. But we now know, from a whole spectrum of clues, that they exist and play an important role in the life of star systems, galaxies, and even the early universe as a whole.

In 2015, the gravitational wave observatory LIGO detected ripples in spacetime which could only be produced by two black holes, spiralling inwards and merging a billion light years away. We’ve known since the 1990s that a supermassive black hole, millions of times heavier than our sun, lurks in the heart of the Milky Way, an achievement recognized by the 2020 Nobel Prize in Physics. And most spectacularly, in 2019, the Event Horizon Telescope stitched together an image of a supermassive black hole, 50 million years old, in the galaxy M87 far, far away:

But for all their astronomical richness and complexity, black holes harbour just as much interest for theoretical physics, and in particular, the program of combining quantum mechanics with gravity, known as quantum gravity. The goal of this tutorial will be to explore some of the problems of black holes and quantum gravity, and to introduce cutting edge approaches to these problems from the language of quantum computing. Rather than give a traditional primer and then laboriously translate into this language, we’ll present black hole physics as a series of computational slogans.

Black holes store physical information

Our first slogan is simply that black holes store physical information. To make a black hole, you need to collapse some matter, like an old star or dust clouds in the galactic core, and this matter contains information: namely, the information about the state it was in when you collapsed it. To make the analogy to computing explicit, suppose we have $N$ classical bits, which can be either $0$ or $1$, say electrons which can be spin up or spin down. We then use an electromagnetic trash compactor to squish them until they form a black hole. The state of the system before it collapsed was an $N$-bit string, and afterwards, those $N$ bits are somehow stored inside the black hole.

If our system is quantum, with $N$ qubits in some state $|\psi\rangle$, then after collapse $|\psi\rangle$ is somehow stored in the black hole. The story is basically the same.

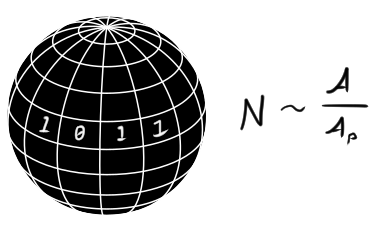
A natural question is how the information stored in the black hole is related to its physical properties, things we can measure. In the 1970s, Jacob Bekenstein and Stephen Hawking discovered something remarkable. They learned that the amount of information you can store in a black hole, the number of bits, is proportional to the area of the horizon, that is, the surface area of the black hole as it appears from outside. In fact, up to some numbers we’re not going to worry, it’s the area of the horizon, $\mathcal{A}$, divided by something called the Planck area, which is the unique area you can build out of basic physical constants:

\[\mathcal{A}_P = \frac{\hbar G}{c^3} \approx 2.56 \times 10^{-70} \text{ m}^2.\]

This gives us the license to draw a black hole as a spherical computer whose surface is split into Planck area-sized pixels. Each of these is a classical bit, which can be either $1$ or $0$, or a qubit if we want to go quantum.

Once a black hole has formed, you can throw more things into it, a bit like downloading something onto your computer. In order to accomodate this new data, the black hole must grow bigger! For instance, if we add a single bit (or qubit), then the horizon must grow by at least one Planck area, as this 2D cartoon shows:

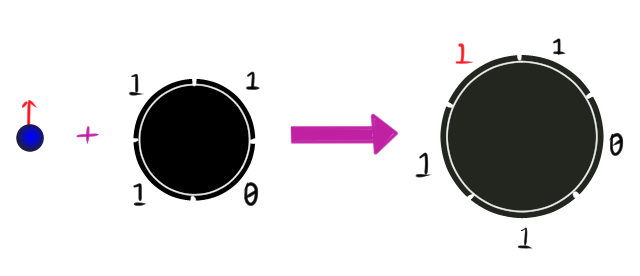
More generally, if we throw $n$ bits (or qubits) into the black hole, the area must grow by at least $n$ Planck areas.

Black holes glow

All of this suggests that information is stored on the surface, so perhaps it can come out again, or at least, create detectable features near the horizon. Guided by this intuition, in 1975 Stephen Hawking made the most ambitious calculation of his life. Using a combination of techniques from gravity and particle physics, he discovered that black holes are not truly black, but glow faintly. This glow is called Hawking radiation, and it costs energy to produce, gradually depleting the black hole until it disappears. This disappearing act is known as black hole evaporation.

But if black holes evaporate, it’s natural to ask what happens to the information they store. Hawking’s calculation suggests that the glow of the black hole is effectively random, a noisy and uninformative process like the light from a hot coal or an incandenscent globe. If this is true, then when black holes form, information is trapped irreversibly behind the horizon, and destroyed when the black hole evaporates. Quantum gravity takes its secrets to the grave, and replaces them with a random sequence of $1$s and $0$s.

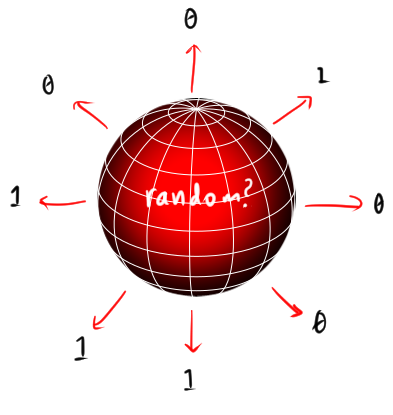
This is kind of a big deal, because destroying information is not allowed by quantum mechanics. Quantum states always evolve in a reversible fashion, which is why gates are reversible in quantum computing. It’s just a basic physical requirement; if you have an irreversible gate, you’ll never be able to built it. So if black holes destroy information, then quantum mechanics must be wrong. This tension between quantum mechanics and Hawking’s glow is called the Information Paradox, and it’s been one of the biggest open problems in quantum gravity for $45$ years.

Black hole encryption

Before we try and solve this, let’s take a step back. Computers usually do more than passively store input data. They will take the data, perform some useful computation on it, then output results, like doing a google search or playing Minecraft. A black hole takes information about collapsing stars, dust clouds, or fatally inquisitive astronauts, and outputs what looks like random noise. Could a reversible computation connect them? Put differently, are there reversible computations which conceal meaningful data as noise? Phrased this way, the Information Problem is really a question about cryptography, the art of secret messages, or more aptly for our purposes, reversibly concealing information.

We can contrast different types of codes. Take something like the Caeser cipher, which simply shifts letters forwards or backwards in the alphabet by some fixed number of places. If we use this to encrypt a long message, it may look like gobbledegook on a first reading, but analyzing how frequently letters occur reveals that they are distributed far from uniformly. By shifting the frequency distribution to match the known frequencies of letters in English, we can easily decrypt. Let’s do an example.

BLA

In contrast, there is a much stronger form of encryption called a one-time pad. The basic idea is to convert a message into a string of binary digits, then