January 5, 2021. Sublets is a fun game for road trips. Take letters from the license plates of passing cars, and find words of which the license plate letters form a subsequence. I explain the game in more detail and provide code for finding solutions. I also explore how the difficulty of the game varies with license plate length, and suggest some easier variants for longer plates.

Introduction

Sublets (standing for “subsequence of letters”) is a game that, to the best of my knowledge, my family collectively invented on a car trip to South Australia in the noughties. In my home state of Victoria, Australia, license plates used to be alphanumeric strings consisting of three letters and three numbers. The game was simply to find a word in which those three letters occurred, and in that order. In mathematical parlance, the license plate letters are a subsequence of the word. Here is an example:

The first person to find a valid word wins the round. The way we played it, if a tie breaker was needed, shorter and/or simpler words were preferred, so “spoof” beat “soporific”.

A solver

I’ve written a little solver to find sublets. It’s based on the nltk (Natural Language Toolkit) package for Python, and in particular, the words corpus, consisting of $\sim 250,000$ English words. It also uses an iterator trick from the itertools library, so we start by invoking these two packages. We also download the corpus:

import nltk
import itertools

nltk.download('words')
from nltk.corpus import words

Our next step is to define a helper function subseq(str1, str2) which checks if str2 is a subsequence of str1. It uses an iterator it over the letters in str2, and then returns True if each letter of the iterator is in str2. The ordering comes for free from the iterator:

def subseq(str1, str2):
  it = iter(str2)
  return all(x in it for x in str1)

Finally, for a given license plate string, sublets(str) simply searches the whole corpus words.words() and looks for supersequences:

def sublets(str):
    return [word for word in words.words()
		if subseq(str, word)]

Note that the words corpus is in lowercase. As an example, we can list words of seven letters or less for which “spf” is a subsequence:

>>> [word for word in sublets('spf') if len(word) < 8]
['sapful', 'scupful', 'shipful', 'shopful', 'skepful', 
	'specify', 'spiff', 'spiffed', 'spiffy',
	'spitful',  'spoffle', 'spoffy', 'spoof',
	'spoofer', 'spuffle', 'stupefy']

Incidentally, this shows that “spoof” is the equal shortest word. In general, we can find the shortest word with subletshort(str). It does two passes through the whole list, one to find the minimum length, and a second to pluck out all the words of that length:

def subletshort(str):
    words = sublets(str)
    minlength = min([len(word) for word in words])
    return [word for word in words if len(word) == minlength]

An example:

>>> subletshort("pwm")
['pewdom']

Apparently, “pewdom” refers to the “system or prevalence of pews in a church”. English is a funny language.

Difficulty scaling

With three letters, the game is often hard, but the chances seem good that a word can eventually be found. At some point, the system changed, and new cars began getting four letters, which seems much more difficult. This raises the question: just how much more difficult is it? The simplest measure is to count the proportion of combinations with answers. This will involve a lot of iteration, so we should optimise a little to make sure things run in a reasonable time. To begin with, we don’t need all the words in the list, just a check if it is non-empty. So we can write a function subletcheck(str) which stops iterating over the corpus and spits out True as soon as it finds a single supersequence:

def subletcheck(str):
    outcome = False
    wordnum = len(words.words())
    i = 0
    while outcome == False & i < wordnum:
        outcome = subseq(str, words.words()[i])
        i = i + 1
    return outcome

We can use this to build a function goodlets(n) which returns the list of strings of length n which have valid supersequences. Rather than iterate over combinations and then words, it iterates over words, adding all the subsequences of length $n$ once again using itertools:

def goodlets(n):
    goodlet = set()
    for word in words.words():
        lower = [combos for combos in
		list(itertools.combinations(word, n)) if
		all(x.islower() for x in list(combos))]
        goodlet.update(set(lower))
    return goodlet

Assuming license plates are random strings of length n, then the chance of success is given by the proportion of good strings to the total number:

def subletprop(n):
    return len(goodlets(n))/float(26**n)

So, let’s check how hard it is! I did up to six letters before my CPU got sore:

>>> [subletprop(n) for n in range(2, 7)]
[1.0, 0.9442, 0.6683, 0.2902, 0.0711]

About 94% of three letter sequences have an answer, but for four letter sequences, this drops to two thirds. As we increase the number of letters, the odds for success are increasingly dire. But these numbers are still much higher than I expected.

Common words

The problem is that the words corpus includes ridiculous items like “spoffle” and “pewdom”. For a more realistic measure, we can replace words with the most common words occurring in a corpus of real text. An oldie but a goodie is the brown corpus, created at Brown University in 1961. I’m going to use it mainly because it’s relatively small, but you can use your favourite nltk corpus. First, we make a list of all the words (with repetition) in the corpus, then obtain a frequency distribution using nltk.FreqDist. We then list the frequencies themselves, and truncate to the most common 20,000 words.

nltk.download('brown')
nltk.download('stopwords')
from nltk.corpus import brown, stopwords

fdist = nltk.FreqDist(word.lower() for word in brown.words()
	if word not in stopwords.words('english'))
freqs = [fdist[word] for word in list(fdist.keys())]
freqs.sort(reverse = True)
cutoff = freqs[20000]
common = [word for word in list(fdist.keys())
	if fdist[word] >= cutoff] + stopwords.words('english')

Note that we’ve used the stopwords corpus to remove common “plumbing” words like “the” or “I” from the frequency distribution, but we add them back in at the end. Our list common gives us the 20,000 most common non-stopwords, plus stopwords. We then go back through the code above and replace words.words() with common. In fact, you can simply define a function genprop(n, lst) which uses an arbitrary list of words. Here are the corresponding chances of success for lst = common:

>>> [genprop(n, common) for n in range(2, 7)]
[0.9822, 0.7606, 0.3264, 0.0635, 0.0056]

This is closer to what I expect. Your chance of getting a four letter combo (eventually) is only one in three. And for five or six letters, forget about it!

Random words

When we plot the probability of sucess for either wordlist, we get an S-shaped sigmoid curve. One family of such sigmoid curves is the exponential sigmoid, of the form:

Here are the datapoints (for words) against a sigmoid with $a = 1.6$ and $b = 4.5$:

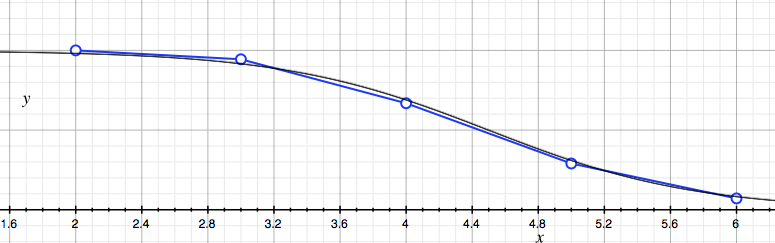
This sigmoid appears to be an artefact of the combinatorics rather than English itself. To see this, we can check against a simple stochastic model of word formation. The basic idea will be to pretend that English is made by selecting letters from the alphabet at random, and if you draw a space, the word terminates. To start with, we import the string and random packages, define the lowercase alphabet, and an alphabet supplemented by some number s of spaces:

import string, random

alpha = string.ascii_lowercase
def alphaspace(s):
    return alpha + s*' '

def rndword(s):
    lett = random.choice(alpha)
    word = lett
    while lett != ' ':
        lett = random.choice(alphaspace(s))
        word = word + lett
    return word[:-1]

We lop off the last character since this is always a space. The number s controls the likelihood of drawing a space. More precisely, the probability of drawing a space is $p = s/(s+26)$, and the length of words follows a geometric disribution, with expected length

English has an average word length of just under five letters, suggesting we should take $s = 9$, with $L_s \approx 4.9$. We can check this empirically by generating many random words and taking the averge length:

def avgrnd(s):
    repeats = 10000
    return sum([len(rndword(s)) for
	i in range(repeats)])/repeats

Let’s see that we get a sensible average:

>>> avgrnd(9)
4.8937

To proceed, we generate a list of 20,000 random words for $s = 9$, and calculate the success probability. The function rndmlst(s, total) generates the list:

def rndmlst(s, total):
    return [rndword(s) for i in range(total)]

Now we check with our function which computes the probability of success given an arbitrary wordlist:

>>> [genprop(n, myrndlst) for n in range(2, 7)]
[1.0, 0.9209, 0.2164, 0.0233, 0.0023]

This dips faster and earlier than the real curves, with $a \approx 3.6$ and $b \approx 3.65$:

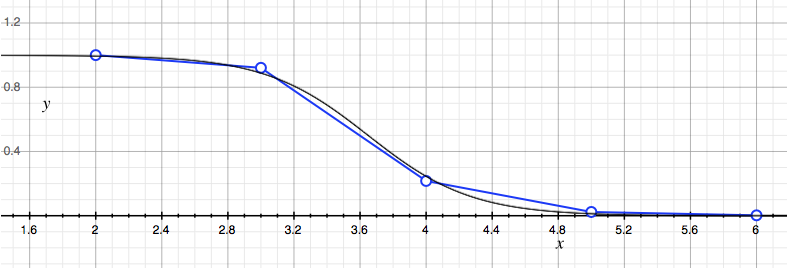
Nevertheless, the sigmoid pops out of our simple random model. It would be nice to derive the explicit form of the curve in this setup, and see what the shape parameters are telling us about the distribution of words, but I leave that for another time.

Subtle sublet variants

Given the basic statistical difficulty of four letters, it would nice to have an easier variant. A simple option is allowing for rearrangment of letters, but penalising the number of swaps. For instance, “mqua” can be rearranged to “aqum” via a single swap (“m” and “a”), and is a subsequence of “aquamarine”. One could also discard letters, e.g. “mqua” becomes “qua”, with supersequence “quantum”. Both necessitate a scoring system, sacrificing some of the simplicity of the original version.

Another, potentially more interesting, option is to pair with license numbers. These could be used as “resources” to shift letters in the alphabet. Since doing this under time pressure, in your head, is difficult, I don’t think any additional scoring mechanism is needed to make this variant fair. To keep things challenging, this works best if numbers are paired with the corresponding letters. Here is an example:

where the overline indicates that a number has been used to move the letter forward in the alphabet. One could restrict to forward shifts, or allow both forward and backward shifts, depending on taste and difficulty. I leave the success probabilities of these variants for another rainy day blog post! Let me know if you have any suggestions for improving the game or your own variants.