December 7, 2016. We list a few desiderata for toting up an infinite list of numbers, and use these to get the “morally correct” answer for some famous divergent series. Extension material for real analysis.

Introduction

Prerequisites: basic calculus and real analysis.

A few months ago, I watched some of Carl Bender’s excellent Perimeter lectures on mathematical physics. One of the pedagogical highlights was a simple method for generalising the textbook definition of convergence. Basically, start by writing down a few simple formal properties of infinite sums, and call anything that satisfies these properties a summation machine. This includes the usual $\epsilon$-$\delta$ notion of convergence of partial sums, but other things as well. In particular, you can use the assumed properties of a summation machine to deduce the formal value of certain famous divergent series (such as $1 - 1 + 1 - 1 \pm \cdots$ and $1 + 2 + 3 + \cdots$). This is a simple way to make the heuristic arguments of Euler and Ramanujan (and latter-day popularisers like Numberphile) somewhat more rigorous. We can summarise it easily:

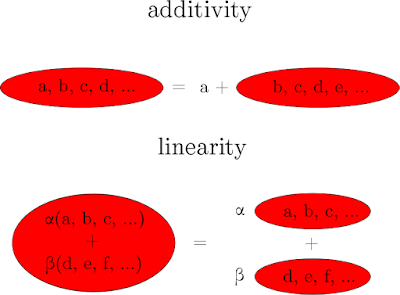A summation machine is a (partial) map from sequences to numbers which is additive and linear (pictured above). Of course, there are more rigorous ways to understand divergent series, but this is a nice way to formally capture some of the moves made in the non-rigorous derivations.

What is a summation machine?

A summation machine is an operator $\mathcal{S}$ which takes a formal sequence of real numbers

\[(a_n) := (a_1, a_2, a_3, a_4, \ldots), \quad a_n \in \mathbb{R},\]

and either (a) spits out a finite real number, or (b) does not give an answer. (Technically, this makes it a partial function.) In the first case, we say that $(a_n)$ converges according to $\mathcal{S}$ or is $\mathcal{S}$-convergent. We call the number it spits out the sum according to $\mathcal{S}$ or $\mathcal{S}$-sum, and write

\[\mathcal{S}(a_n) := \sum_{n\geq 1}^\mathcal{S} a_n.\]

In case (b), we say the series is $\mathcal{S}$-divergent. We impose two further properties on $\mathcal{S}$, which generalise the behaviour of finite sums. Suppose $(a_n)$ and $(b_n)$ converge under $\mathcal{S}$. Then we must have

\[\begin{align*} \sum_{n\geq 1}^\mathcal{S} a_n & = a_1 + \sum_{n\geq 2}^\mathcal{S} a_n & \text{(additivity)}\\ \sum_{n\geq 1}^\mathcal{S} (\alpha a_n + \beta b_n) & = \alpha\sum_{n\geq 1}^\mathcal{S} a_n + \beta\sum_{n\geq 1}^\mathcal{S} b_n . & \text{(linearity)} \end{align*}\]

The first property forces $\mathcal{S}$ to behave like a sum. Thinking of a sequence to be summed as a stack, we can pop off the top item, process the tail of the stack, and add the top item to the result. This is not enough to nail down a notion of convergence, since we can choose to deal with the tail in different ways.

The second property forces $\mathcal{S}$ to obey some simple limit algebra. Another way to view the second property is the statement that summation machines $\mathcal{S}$ are linear transformations (in fact, linear functionals) on the space of real sequences, considered as vectors with an infinite number of components. (Requiring $\mathcal{S}$-convergence complicates this statement a little, but it is morally correct.)

Exercise. (a) Using induction, show that applying a summation machine to a finite sequence $(a_n)$ (that is, $a_n = 0$ for all $n$ bigger than some $k$) just gives the usual finite sum. (b) Show that additivity and linearity are equivalent to a single property:

\[\sum_{n\geq 1}^\mathcal{S} (\alpha a_n + \beta b_n) = (\alpha a_1 + \beta b_2) + \alpha\sum_{n\geq 2}^\mathcal{S} a_n + \beta\sum_{n\geq 2}^\mathcal{S} b_n.\]

(c) Give an example of a linear functional on the space of real sequences which is (i) linear but not additive; (ii) additive but not linear.

Cesàro and Borel summation

Let’s give a couple of examples of summation machines. The first is just the “textbook” notion of the limit of partial sums:

\[\mathcal{T}(a_n) := \lim_{N\to\infty}\sum_{n=1}^N a_n := \lim_{N\to\infty} A_N\]

where we introduce the notation $A_N$ for the $N$-th partial sum. It’s not hard to see that this is additive and linear; we check the first property and leave the second as an (easy) exercise. From limit laws, we have

\[\mathcal{T}(a_n) = \lim_{N\to\infty}\sum_{n=1}^N a_n = \lim_{N\to\infty}\left(a_1 + \sum_{n=2}^N a_n\right) = a_1 + \lim_{N\to\infty}\sum_{n=1}^{N-1} a_{n+1}.\]

This is what was required. This notion of convergence is useful and historically important, but somewhat rigid.

A more flexible method is Cesàro summation $\mathcal{C}$. The Cesàro sum is just the average of the first $k$ partial sums as $k \to \infty$:

\[\mathcal{C}( a_n) \equiv \lim_{k\to\infty} \frac{1}{k}\sum_{N=1}^k A_N,\]

Clearly this is a map of the right sort. Linearity just follows from the linearity of limits and partial sums, so let’s check additivity:

\[\begin{align*} \mathcal{C}( a_n) & = \lim_{k\to\infty} \frac{1}{k}\sum_{N=1}^k A_N\\ & = \lim_{k\to\infty} \frac{1}{k}\sum_{N=1}^k \left(A_N - a_1 + a_1\right)\\ & = \lim_{k\to\infty} \frac{1}{k}\left(ka_1 + \sum_{N=1}^k \left(A_N - a_1\right)\right)\\ & = a_1 + \lim_{k\to\infty} \frac{1}{k}\sum_{N=1}^k A_N' = a_1 + \mathcal{C}(a_{n+1}), \end{align*}\]

where $A_N’$ denotes the $N$-th partial sum with respect to the modified sequence $a_2, a_3, \ldots$. Done!

Exercise. (a) Define Borel summation by

\[\mathcal{B}(a_n) := \int_0^\infty \sum_{n=0}^\infty dt \,e^{-t} \frac{a_n t^n}{n!}.\]

Show that Borel summation is linear and additive. (c) Is Grandi’s series (see below) $\mathcal{B}$-convergent?

Some divergent series

At this point, we can apply these notions to some famous divergent series. First, Grandi’s series, where we must sum the sequence $a_n = (-1)^{n+1}$. It’s not hard to show that it is Cesàro-convergent.

Exercise.. Prove Grandi’s series has Cesàro of $1/2$.

Let us recapitulate the heuristic argument using summation machines. Suppose that $a_n$ is $\mathcal{S}$-convergent for a summation machine $\mathcal{S}$, with $s := \mathcal{S}(a_n)$. Then, from additivity and linearity,

\[1 - s = 1 - \sum_{n\geq 1}^\mathcal{S} (-1)^{n+1} = 1 - 1 + \sum_{n\geq 2}^\mathcal{S} (-1)^{n} = \sum_{n\geq 1}^\mathcal{S} (-1)^{n+1} = s.\]

Thus, $s = 1/2$ for any summation machine $\mathcal{S}$ for which $a_n$ is $\mathcal{S}$-convergent. This uses the same reasoning as the heuristic proof, but is a general result about notions of convergence! I think this is pretty neat. We let the reader prove a similar statement about the sum of natural numbers as an exercise.

Exercise (sum of natural numbers). (a) Consider the alternating sum of natural numbers,

\[1 - 2 + 3 - 4 + \cdots +(-1)^{n+1}n + \cdots\]

Assuming this sum and Grandi’s series are $\mathcal{S}$-convergent, show that

\[\sum_{n\geq 1}^\mathcal{S} (-1)^{n+1} n = \frac{1}{4}.\]

(b) Deduce that

\[\sum_{n\geq 1}^ \mathcal{S} n = -\frac{1}{12}.\]

Hint: Use part (a), linearity, and $L - 4L = -3L$, where $L$ is the limit.

Conclusion

There are various questions we can ask about this basic setup. Can we always find a way to “tame the tail” of a given divergent series? We gave the example of Grandi’s series and Cesàro summation above, but for the sum of natural numbers, there is (as far as I know) no summation machine which gives the “correct” answer $-1/12$. If we relax our restrictions on summation methods, we can obtain this result using Euler-Maclaurin regularisation and related objects like the Riemann zeta function. Still, from a pedagogical standpoint, summation machines are a nice entrée to divergent series, encouraging us to think a little more deeply about the algebraic properties used in heuristic proofs.