Introduction

Prequisites: basic quantum mechanics, relativity, and logic gates; some topology.

CTCs are physically interesting since they appear in solutions to Einstein's field equations, most famously the Gödel metric. They are philosophically interesting since they give rise to paradoxes of time travel, most famously the grandfather paradox:

In fact, Gödel invented his solution to prove a philosophical point to Einstein. Consistency seems to impose extreme and unnatural constraints on the time traveller. In physical language, a time traveler's boundary conditions are rather stringent! David Deutsch wrote a great paper (1991) where he adds quantum mechanics to the mix and figures out how the physical/philosophical picture changes.

CTC as a logic gate

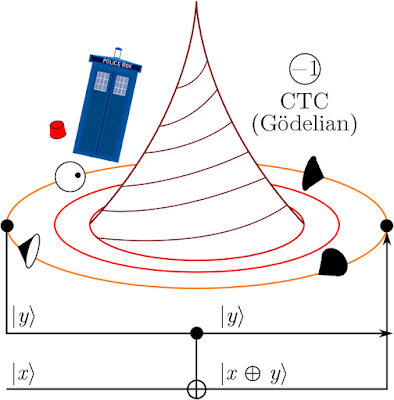
Deutsch's big idea was to embed the CTC as a module in a quantum computer. This lets us reason about the local/computational features of CTCs instead of the global/geometric properties tracked by general relativity. Thought of as a logic gate, a CTC takes a qubit and spits it out earlier in time. For this reason, we label it by $-1$.

A computer is a system of identical particles (qubits) which move along designated paths and interact at reversible gates. Paths are represented by lines and gates by boxes. We assume we have a two-level system with labels in $\mathbb{Z}_2$ (mod 2). The state space is $H = \mbox{span}_\mathbb{C}\mathbb{Z}_2$. To implement the paradox (G) on a computer, attach a CTC to a CNOT gate $G$, i.e., set up the circuit below:



The large arrow at the bottom represents time. An incoming qubit $|x\rangle$ enters $G$ and interacts with $|y\rangle$, an older version of itself. The output of the interaction $|x \oplus y\rangle$ leaves $G$ and travels through the CTC to become the old qubit. The looped particle reenters $G$, interacts with the younger qubit, and finally leaves $G$ altogether. Think of $|x\rangle$ as a time traveller to see why the circuit takes this form!

The Hilbert space for $2$-qubit input states is the tensor product $H \otimes H$. We define the tensor product of elements
\begin{align*}
  (\alpha |0\rangle + \beta|1\rangle) \otimes (\alpha' |0\rangle +
  \beta'|1\rangle) & \equiv \alpha\alpha'|00\rangle + \alpha\beta'|10\rangle + \beta\alpha'|10\rangle + \beta\beta'|11\rangle.
\end{align*}Recall that a separable state $|\psi\rangle$ satisfies $|\psi\rangle  = |\psi_1\rangle\otimes |\psi_2\rangle$ for some $|\psi_1\rangle, |\psi_2\rangle\in H$; otherwise, it is entangled. Since $H\otimes H$ has a separable basis, we can (and do) lazily define linear maps for separable states only.

Classical consistency

We start by classically analysing the paradox. For computational basis elements, $G$ stores the sum
mod 2 (XOR) in the first output and passes the old ket into the second:
\[
|x\rangle |y\rangle \overset{G}{\longrightarrow} |x \oplus y\rangle |y\rangle, \quad x,
y\in\mathbb{Z}_2.
\]Consistency means that the particle entering the CTC leaves it, or $x \oplus y = y$, which implies $x = 0$. This is a computational analogue of (G): $|1\rangle$ can never enter $G$! But, in quantum land, why assume that $|y\rangle$ is a classical basis element? If $|y\rangle$ is a superposition, consistency may not force $x = 0$.

Density matrix formalism

To pursue this idea, we can use density operators. For an ensemble which produces different states $|\psi_i\rangle$ with probabilities $p_i$, the density matrix is
\[
\textstyle \hat{\rho} \equiv \sum_i p_i |\psi_i\rangle\langle\psi_i|.
\]It turns out that $\hat{\rho}$ is a density matrix if and only if

• $\langle \psi| \hat{\rho}| \psi\rangle \geq 0$ for any state $|\psi\rangle$, so $\hat{\rho}$ is a positive operator; and
• $\mbox{Tr}[\hat{\rho}] = 1$.

It follows that the mean of a finite number of density operators is a density operator. For reversible gates, state vectors evolve as $|\psi_i\rangle \to U|\psi_i\rangle$ for some unitary $U$. It follows that $\hat{\rho}$ evolves as \[
\textstyle \hat{\rho} \overset{U}{\longrightarrow} \sum_i p_i
U|\psi_i\rangle\langle\psi_i|U^\dagger = U \hat{\rho} U^\dagger.
\]For a separable state in $H\otimes H$ with subsystem densities $\hat{\rho}_1$ and $\hat{\rho}_2$, the joint density $\hat{\rho} \equiv \hat{\rho}_1 \otimes\hat{\rho}_2$ is defined by
\[
\hat{\rho} (|\psi_1\rangle\otimes|\psi_2\rangle) = \hat{\rho}_1|\psi_1\rangle \otimes \hat{\rho}_2|\psi_2\rangle.
\] Finally, we define the partial trace $\mbox{Tr}_1$ (with $\mbox{Tr}_2$ similar):
\[
\mbox{Tr}_1(|\psi_1\rangle\langle\psi_1|\otimes |\psi_2\rangle\langle\psi_2|) = \langle\psi_1|\psi_1\rangle|\psi_2\rangle\langle\psi_2|.
\] From a joint density matrix $\hat{\rho}$, we find the density matrix for subsystem 2 by tracing away the first part, $\hat{\rho}_2 = \mbox{Tr}_1\hat{\rho}$, with similar remarks $\hat{\rho}_1$ similar. Note that $\mbox{Tr}_2\hat{\rho} \otimes \mbox{Tr}_1\hat{\rho} = \hat{\rho}$ only if the state is separable. The motivation for the partial trace is that it works! See Nielsen and Chuang (2000) for more details.

Quantum consistency

Suppose the young ket is in an arbitrary state $|\psi\rangle$, with density matrix $|\psi\rangle \langle\psi|$. If the old input ket has density matrix $\hat{\rho}$, the joint density matrix is $|\psi\rangle \langle\psi| \otimes \hat{\rho}$. The gate $G$ evolves this joint density via some unitary
operator $U_G$ as
\[
|\psi\rangle \langle\psi| \otimes \hat{\rho} \longrightarrow U_G(|\psi\rangle \langle\psi| \otimes \hat{\rho}) U^\dagger_G.
\] Consistency means that the young density matrix leaving the gate is the old density matrix as it enters, or
\begin{equation}
\mbox{Tr}_2[U_G(|\psi\rangle \langle\psi| \otimes \hat{\rho}) U^\dagger_G] = \hat{\rho}.\tag{1}
\end{equation} You can find such a $\hat{\rho}$ for any $|\psi\rangle$, so consistency doesn't constrain $|\psi\rangle$. (For instance, if $|\psi\rangle = |1\rangle$, $\hat{\rho} = \tfrac{1}{2}\mathbf{I}$ works. This implies the loss of unitarity, which may seem crazy, but can be interpreted fairly naturally in the many-worlds approach.) We'll show how to extend this result to any reversible gate below. It follows that there is no grandfather paradox for qubits!

Fixed points

If we generalise $U_G$ to unitary $U$ (for two $n$-qubit inputs), and $|\psi\rangle\langle\psi|$ to $\hat{\rho}_{in}$, we see from $(1)$ that $\hat{\rho}$ solves the consistency problem just in case it is a fixed point of the operator
\[
\mathsf{S}(\hat{\rho}) = \mbox{Tr}_2[U(\hat{\rho}_{in} \otimes \hat{\rho}) U^\dagger].
\]Deutsch showed that all such operators have fixed points. Why? For intuition, suppose we connect an infinite sequence of identical gates; piping qubits through it will be a stationary, memoryless process like a Markov chain. But run a Markov chain long enough and (except in pathological cases) it stabilises to some state, a fixed point of the Markov chain. But let's prove it properly.

Consider $\mathsf{S}$ as defined above. We must show that $\mathsf{S}$ has a fixed point for any choice of $U$ and $\hat{\rho}_{in}$. Pick an arbitrary density matrix $\hat{\rho}$, and define
\[
\textstyle \hat{\rho}_N = (N+1)^{-1}\sum_{n=0}^N \mathsf{S}^n\hat{\rho}.
\] This is a mean of density operators, hence a density operator. Note that $\mbox{Tr}\,\hat{\rho}^2 \leq 1$ for any density matrix $\hat{\rho}$, and $\mbox{Tr}(A^\dagger B) = \langle A,B\rangle$ is an inner product and therefore satisfies the Cauchy-Schwarz inequality. Hence,     \begin{align*}
      0 & \leq \mbox{Tr}[(\mathsf{S}\hat{\rho}_N - \hat{\rho}_N)^2] \\
      & =
      (N+1)^{-2}\mbox{Tr}[\textstyle{(\sum_{n=0}^N\mathsf{S}^{n+1}\hat{\rho}
        - \mathsf{S}^{n}\hat{\rho})^2]} \\
      & = (N+1)^{-2}\mbox{Tr}[(\mathsf{S}^{N+1}\hat{\rho} -
      \hat{\rho})^2]
      \\
      & = (N+1)^{-2}\mbox{Tr}[(\mathsf{S}^{N+1}\hat{\rho})^2 - 2
      \hat{\rho}\,\mathsf{S}^{N+1}\hat{\rho} + \hat{\rho}^2] \\
      & \leq (N+1)^{-2}[\mbox{Tr}(\mathsf{S}^{N+1}\hat{\rho})^2  + 2
      (\mbox{Tr}(\mathsf{S}^{N+1}\hat{\rho})^2\mbox{Tr}\hat{\rho}^2)^{1/2}
      + \mbox{Tr}\hat{\rho}^2] \\ & \leq \frac{4}{(N+1)^{2}}.
    \end{align*} The set of density operators is compact, so the sequence $\{\hat{\rho}_n\}$ has an accumulation point $\hat{\rho}^*$. We pick a subsequence $\{\hat{\rho}_{n'}\}$ converging to $\hat{\rho}^*$, and note from the inequality above and the continuity of $\mbox{Tr}\,\hat{\rho}^2$,
\begin{align*}
\lim_{n'\to\infty} \mbox{Tr}[(\mathsf{S}\hat{\rho}_{n'} -
\hat{\rho}_{n'})^2] = 0 & \,\,\Rightarrow \,\,
\mbox{Tr}[(\mathsf{S}\hat{\rho}^* - \hat{\rho}^*)^2] = 0 \,\, \Rightarrow \,\, \mathsf{S}\hat{\rho}^* =
\hat{\rho}^*.
\end{align*} In other words, $\hat{\rho}^*$ is a fixed point of $\mathsf{S}$. We're done!

Other points of interest

The Doctor (pictured below) is not a qubit: a time-traveller is a classical rather than a quantum object.
So Deutsch's "resolution" of the grandfather paradox may not help. On the other hand, if (as Deutsch thinks) the many-worlds interpretation of quantum mechanics is correct, classical objects would also be able to avoid (G). The CTC would act as a sort of gateway between Everitt universes, letting a time-traveller switch between superposed states. If they existed, CTCs would let us test interpretations of QM!

In computational terms, a CTC is a magic box which finds fixed points of evolution operators in constant time. For this reason, Deutsch's paper kickstarted research on complexity and CTCs. To the best of my (limited) knowledge, the most striking result in the area is due to Aaronson and Watrous (2009), who proved that CTCs make classical and quantum computing equivalent. CTCs would allow classical computers to efficiently simulate quantum computers. (Basically, a CTC turns polynomial space into polynomial time, allowing classical computers to efficiently simulate quantum computers.)

For more fun stuff, read Deutch's paper!

References

• "Quantum mechanics near closed timelike lines'' (1991), David Deutsch. Phys. Rev. D, 44(10):3197-3217.
• Quantum Computation and Quantum Information (2000), Michael Nielsen and Isaac Chuang. CUP.
• "Closed timelike curves make quantum and classical computing equivalent'' (2009), Scott Aaronson and John Watrous. Proc. R. Soc. A, 465:631-647.