June 22, 2015. A quick post on a beautiful family of graphs, and the new masters course at Oxford.

The Petersen family

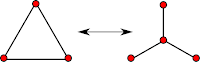
The Petersen family is an elegant set of graphs related by the Δ-Y transformation. This replaces a 3-cycle (Δ) with a 3-point star (Y), or vice versa:

We start with the Petersen graph (hence the nomenclature), and fill out the orbit under Δ-Y transformations. This orbit turns out to be finite, as can be laboriously verified. The orbit is pictured below, with the Petersen graph at the bottom and transformations represented by blue edges.

Image due to graph theorist and prolific Wikipedian David Eppstein.

Robertson, Seymour and Thomas (1993) proved that the Petersen family is the set of forbidden minors for linklessly embeddable graphs in 3-space. In other words, a graph can be embedded in 3-dimensional Euclidean space without links (interlinked loops) if and only if we cannot delete edges and contract vertices so that we end up with a member of the Petersen family.

This characterisation of a class of graphs in terms of forbidden minors is a special case of a very deep theorem proved in 2004 by Robertson and Seymour, the graph minor theorem. Any set of graphs closed under the taking of minors has a finite set of forbidden minors! Enumerating forbidden minors is typically very hard. For more details, Diestel’s text Graph Theory is a good place to start. But mainly, I just wanted an excuse to show David Eppstein’s awesome picture!

New course at Oxford

The University of Oxford is set to offer a new masters course in mathematical and theoretical physics, the MMathPhys. Based on the course guide, it resembles the Part III at Cambridge but with less maths and perhaps a slightly wider range of physics. The handbook is written in endearingly stuffy Oxbridge prose, and includes silly latinate titles for different specialisations, e.g.,

SUPERCORDULA = hard-core string theorist
DURACELLA = hard-core hard condensed matter theorist
GAIA = geophysicist/climate physicist
COMPLICATA = complexity scientist.

Jokes aside, this seems like an exciting variation on the Part III theme.